自制NavMesh2D（一）

Medemus

Navigation

发布于：2020年11月2日

次浏览

图源：https://www.pixiv.net/artworks/84705376

网格构建

三角形剖分

三角形剖分的方法有好几种例如Delaunay三角剖分算法

1
2
3
4
5

1.除了端点，三角形的边不包含其他任何点。

2.除了在点上的连接，没有任何一条边是相交的。

3.所有的面都是三角形，且所有三角形的合集是所有点集合的凸包。

但是这个方法里的几种算法都只适合于凸多边形，而真实情况则是会出现凹多边形以及空洞等情况。
所以使用切耳算法能够更好的解决这些问题。

1
2
3
4
5

第一，找到一个耳点。

第二，记录这个耳朵三角形，然后去掉这个耳朵点，在剩余的顶点中，继续回到第一步

第三，直到剩下最后3个点形成一个三角形并记录下来，把所有记录的三角形拼接起来就形成了三角化网格。

上述步骤的几个名词解释:

1
2
3
4
5

1.简单多边形是，所有顶点都是顺时针或者逆时针排列的顶点，每个顶点只连接两条边，边与边之间没有交叉的多边形，就叫做简单多边形。

2.耳点，耳点的意思是，多边形中相邻的三个顶点V0,V1,V2形成的三角形里，不包含任何的其他顶点，并且如果V1点是凸点，即V0-V1的连线与V1-V2的连线之间形成的夹角小于180度，则认为V1是耳点。所以一个由4个顶点组成的多边形中，至少有2个耳点。

3.耳朵三角形，三角形顶点中有耳点的就叫耳朵三角形。

如果出现了空洞的话:

1
2
3

1，用外围的简单多边形上的点，连接‘洞’的简单多边形，因此为了保持所有点的一致性，‘洞’必须是与外围的多边形的点的顺序是相反的。即外围如果是逆时针的顺序，‘洞’则需要顺时针的顺序。

2，在连接处，产生两个一模一样的点，即连接点。

下面以图片来做演示:

不包含洞与岛

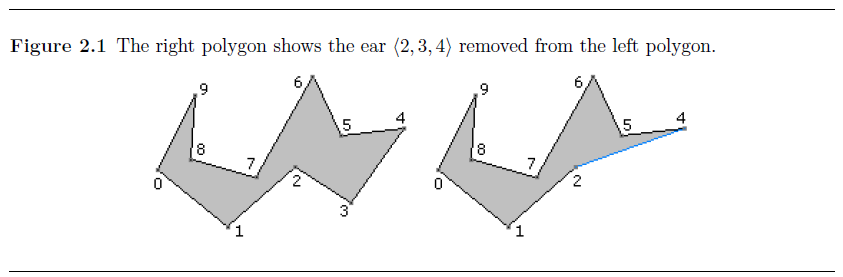
首先初始的时候凸顶点集合C={0,1,3,4,6,9}，初始凹顶点集合R={2,5,7,8},初始的耳朵集合E={3,4,6,9}(三角形0,1,2中间有一个顶点7,所以1不是耳朵)。
然后将顶点3去除后,2还是凹顶点,4还是耳朵顶点,所以这两集合不变。

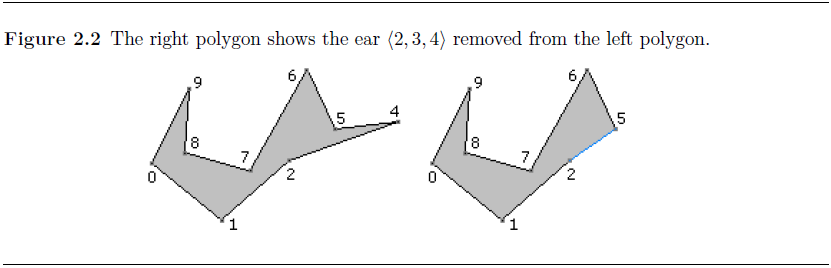
接着移除4,5从凹顶点变成了凸顶点,并且成为了耳朵,所以将5从凹顶点移除,加入耳朵顶点集合。
凹节点集合R={2,7,8},耳朵集合E={5,6,9}

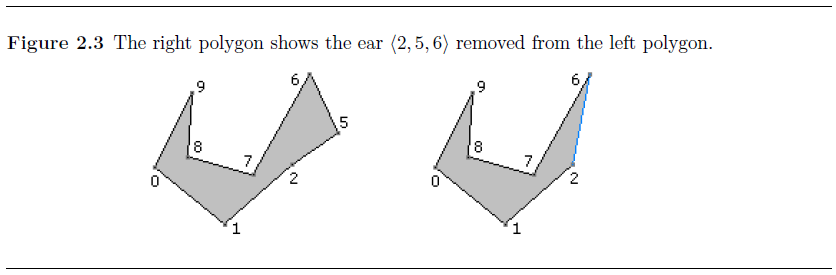
移除5,此时2变成了凸顶点,但由于7在<1,2,6>中,所以不是耳朵,R={7,8}(移除了2)，耳朵集合E={6,9}(移除了5)。

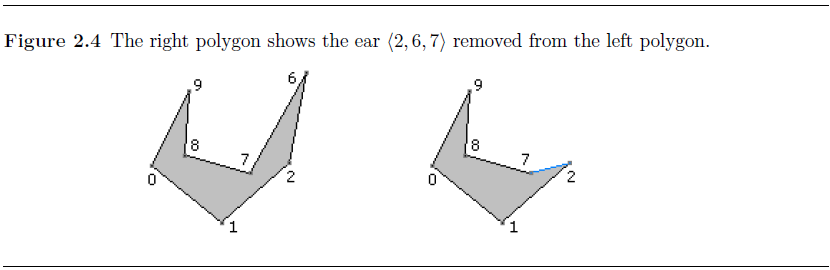
此时2变成了耳朵,耳朵集合E={9,2}(添加2移除6)。

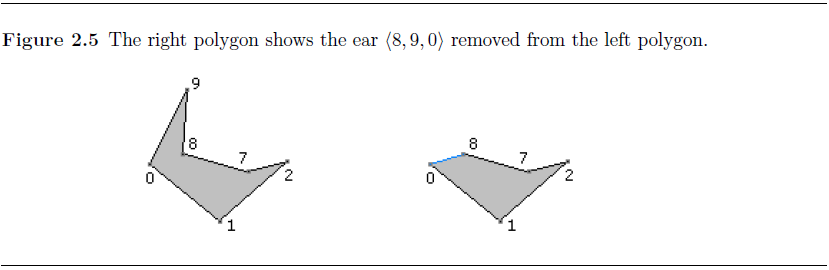
8变成了耳朵,0也从凸节点变成了耳朵,凹点集合R={7}，耳朵集合E={0,2,8}(添加8 ，添加0，移除9)。

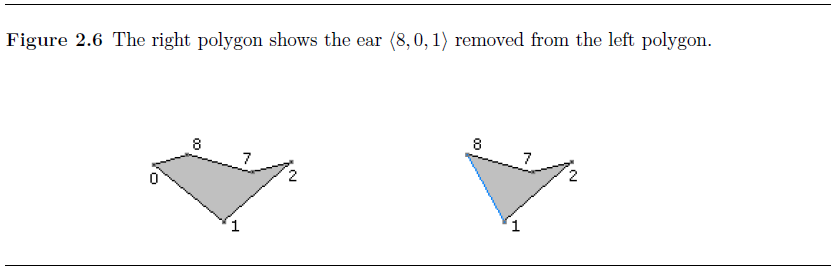
耳朵列表变为E={2,8}(移除了0)。

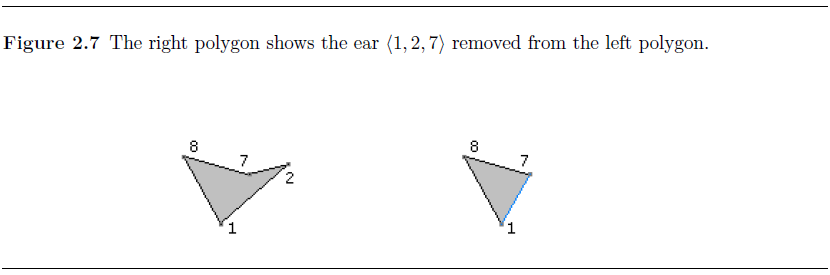
只剩下了三个顶点,组成最后一个三角形。

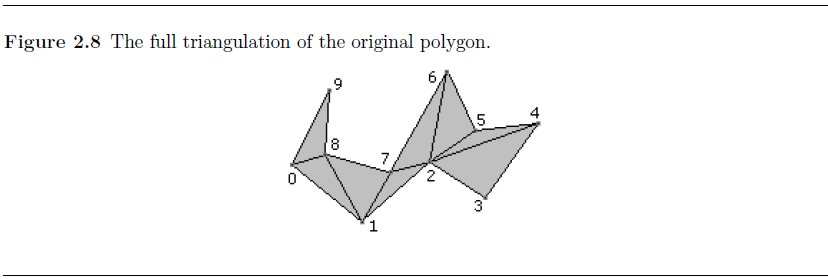
含有洞与岛的情况

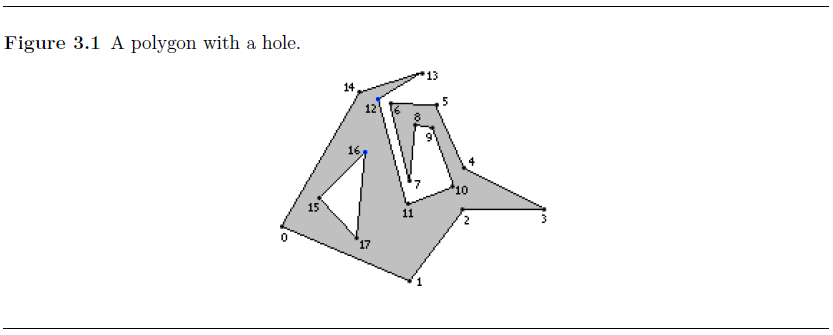
注意:外侧多边形的定点方形和内测岛洞的顶点方向必须是相反的。如果外侧的顶点是逆时针顺序，那么内测的顶点则必须是顺时针顺序。

首先将其构造成简单多边形,连接<11,16>,同时复制这两点连接<19,18>,两条边重合,方向相反,以此将该多边形构造成简单多边形,去除了空洞。

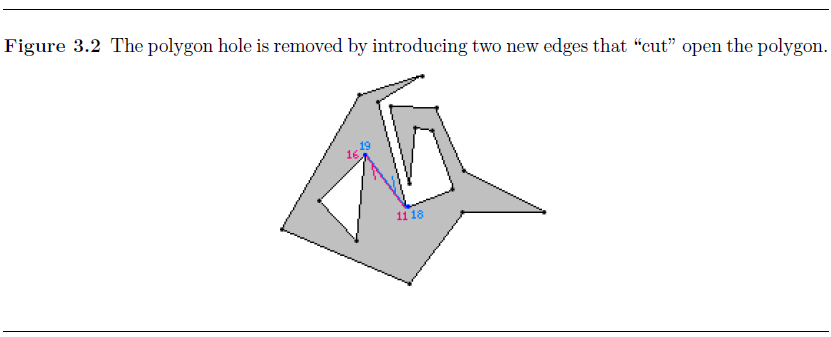
图中蓝色的顶点是互相可见的,在顶点数据结构不同的情况下,互相可见的顶点必须复制。每个数据结构存储当前点可能是凹点也可能是凸点。即使使用同一个坐标的两个点，也可能一个是凹点，一个是凸点，比如位于最下面的蓝色顶点11(18)。原始的顶点在最初的外多边形中是凹点，分割后在新的多边形中，V11与红色边相连，构成了一个凹点，与蓝色边相连构成另一个凸点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

原始的外多边形顶点数据：

{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14}

原始的内多边形数据

{15,16,17}

分割后顶点V11被复制出V18，顶点V16复制出V19，这时候的简单多边形数据如下：

{0,1,2,3,4,5,6,7,8,9,10,11,16,17,15,19,18,12,13,14}

新的多边形即可以使用耳朵裁剪法切割。

寻找互相可见点

上图中，11与16是一对相互可见点，但其实这样的点不止其一对，一个点来自外多边形，一个点来自内多边形，所以需要一个算法来寻找这样的多边形点。

以内多边形的最右点(X最大的点)为原点，向右作射线，如首先交于外多边形的顶点，则该顶点为相互可见点，而一般会相交于边上一点，设相交于I点，该边两端点离M(原点)最近的点就是相互可见点。

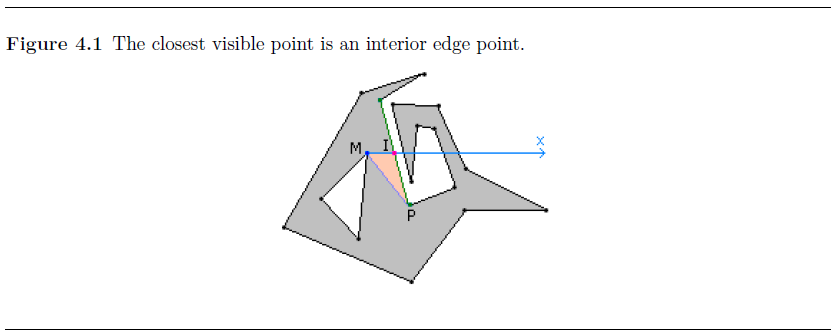
但有时候可能会出现被阻挡的情况。

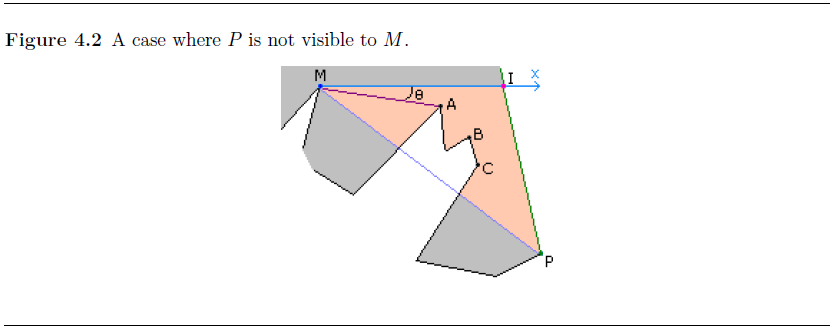
此时有A、B、C三点在三角形MIP内部，获取这三点与M的连线与MI的夹角，取夹角最小的为互相可见点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

算法总结如下:

1、寻找内部多边形x周最大值的顶点M

2、沿X周正方向，寻找最近的相交边<Vi,Vi+1>,让其焦点设置为I，构成X轴方向对M的最近可见点

3、如果I是一个外部顶点，则M和I相互可见，算法执行结束

4、如果I只是边上的一个点，寻找端点中x值片的一个，设置为P

5、寻找位于P内的其他外多边形的可连接顶点。如果所有的顶点都在<M,I,P>之外，则M与P相互可见，反正结果

6、如果有至少一个点位于三角形<M,I,P>内部，则寻找其中的一个顶点，计算其与x轴(1,0)的夹角，夹角最小的顶点R与M构成相互可见边，算法结束

7、在这个算法中，有可能有多个顶点同事具有最小的角度，这种情况下，寻找距离M最近的一个点即可

含有多个岛洞的多边形

此处的岛洞都仅被外多边形包含，彼此不存在嵌套岛洞的情形

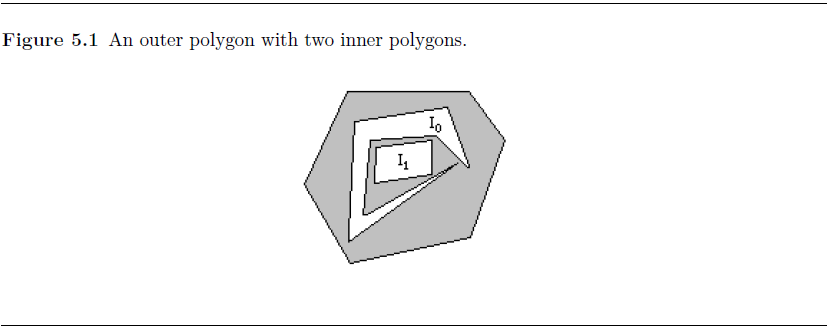
内多边形I1没有任何一个顶点与外部多边形相互可见，多边形I0则拥有多个与外部多边形相互可见的点。因此，我们可以使用前面介绍的算法，首先把I0和外部多边形拆分，合并成为一个简单多边形，这样，新形成的外多边形则和I1构成了一件简单多边形，使用耳切法分割集合。

嵌套多边形

内多边形也可能包含一些泪如岛洞的外多边形，类如嵌套。这样导致了嵌套多边形的树形结构。根节点是最外围的外多边形，子节点则是包含在当前最外多边形内部的内多边形。每一个孙子节点，则是构成直接被最外围多边形包含的内多边形的子树，每个多边形树可以按照宽度优先去遍历。

使用上面的获取互相可见边的方法，可以生成新的简单多边形，对每个内多边形都做这样的操作，完成最终的三角划分，以便获取最终的索引顺序，来代替最初的多边形顶点定义顺序。相比原始的值，这里可能需要复制一些顶点，以便被多个三角形使用。

更新于：2021年3月11日

NavMesh

Navigation