自制NavMesh2D（二）

Medemus

Navigation

发布于：2020年11月4日

次浏览

图源：https://www.pixiv.net/artworks/85217491

根据上面的学习，能够大致了解一个NavMesh2D的制作流程了，所以接下来就是上手实践。
在此参考了Unity3D架构设计NavMesh寻路的设计。

根据顶点生成多边形

由于所制作的为纯2D，是可以由sprite的顶点信息获取边缘信息的，所以在此我想先跳过光栅化的阶段，先行从多边形生成开始。

在此需要制定多边形类的信息，在此设定的多边形类的参数为List<Vector>类型的顶点列表。

public class Polygon
    {
        public List<Vector2> points;

        public Polygon()
        {
            points = new List<Vector2>();
        }
        public Polygon(List<Vector2> vertices)
        {
            points = new List<Vector2>();
            foreach (var vertex in vertices)
            {
                points.Add(vertex);
            }
        }
        public Polygon(Vector2[] vertices)
        {
            points = new List<Vector2>();
            foreach (var vertex in vertices)
            {
                points.Add(vertex);
            }
        }
    }

有了点就该有线了，那么线应该就是由一个起点与一个终点所组成。

public class Line
    {
        public Vector2 start;
        public Vector2 end;

        public Line(Vector2 start, Vector2 end)
        {
            this.start = start;
            this.end = end;
        }
    }

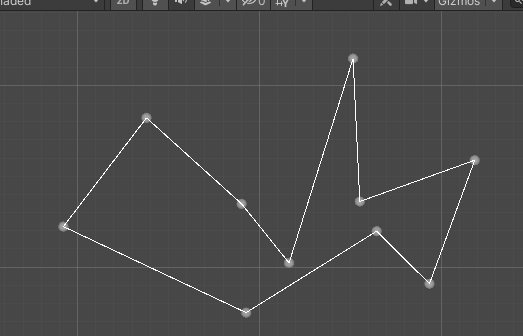
然后只要规定一个连线顺序（在这我规定的是外多边形为顺时针，内多边形为逆时针），就可以描述一个多边形了。

用Gizmo来绘制测试一下

对单个多边形进行三角形剖分

多边形有了后，就该着手进行剖分了，先不考虑存在空洞、相交的情况。

为了进行剖分，首先需要构建三角形类，三角形的组成和多边形类似，但为了进行一些操作所以需要更多的参数。

public class Triangle
    {
        public Vector2[] points;//顶点列表
        public int ID;//每个三角形的ID
        public int[] neighborID;//三角形邻居节点ID
        public Vector2 center;//中心点
        
        public Triangle()
        {
            points = new Vector2[3];
            neighborID = new int[] { -1, -1, -1 };
            center = Vector2.zero;
        }
     
        public Triangle(Vector2 pos1,Vector2 pos2,Vector2 pos3,int id)
        {
            points = new[] {pos1, pos2, pos3};
            ID = id;
            neighborID = new[] {-1, -1, -1};

            center.x = (points[0].x + points[1].x + points[2].x) / 3;
            center.y = (points[0].y + points[1].y + points[2].y) / 3;
        }
    }

在剖分前，还需要几个工具类进行辅助操作。

在工具类Util中，添加以下方法：

/// <summary>
/// 获取多边形在三角形内部的点
/// </summary>
public static bool TryGetInnerPoints(Triangle triangle,Polygon polygon,out List<int> res)
{
    res = new List<int>();
    List<Vector2> points = polygon.points;
    HashSet<Vector2> trianglePoints = new HashSet<Vector2>(triangle.points);
    for (int i = 0; i < points.Count; i++)
    {
        if (!trianglePoints.Contains(points[i]))
        {
            if (MUtil.IsPointIn(points[i], triangle))//是否有点在三角形内部
            {
                res.Add(i);
            }
        }
    }
    if (res.Count > 0)
        return true;
    return false;
}

/// <summary>
/// 指定点是否在三角形中
/// </summary>
public static bool IsPointIn(Vector2 point,Triangle triangle)
{
    Vector3 AB = triangle.points[1] - triangle.points[0];
    Vector3 AC = triangle.points[2] - triangle.points[0];
    Vector3 AP = point - triangle.points[0];

    float ABAB = Vector3.Dot(AB, AB);
    float ABAC = Vector3.Dot(AB, AC);
    float ABAP = Vector3.Dot(AB, AP);
    float ACAC = Vector3.Dot(AC, AC);
    float ACAP = Vector3.Dot(AC, AP);

    float inverDeno = 1 / (ABAB * ACAC - ABAC * ABAC);

    float u = (ACAC * ABAP - ABAC * ACAP) * inverDeno;
    if (u < 0 || u > 1)
    {
        return false;
    }
    float v = (ABAB * ACAP - ABAC * ABAP) * inverDeno;
    if (v < 0 || v > 1)
    {
        return false;
    }

    return u + v <= 1;
}

在三角形类中，添加方法：

/// <summary>
/// 获取三角形的指定边
/// </summary>
/// <param name="index"></param>
/// <returns></returns>
public Line GetLineByIndex(int index)
{
    Line line;

    switch (index)
    {
        case 0:
            line = new Line(this.points[0], this.points[1]);
            break;
        case 1:
            line = new Line(this.points[1], this.points[2]);
            break;
        case 2:
            line = new Line(this.points[2], this.points[0]);
            break;
        default:
            line = new Line(this.points[0], this.points[1]);
            break;
    }

    return line;
}

为了获取三角形之间的关系，所以需要有

/// <summary>
/// 获取与指定三角形相邻的边
/// </summary>
public bool TryGetNeighbor(Triangle triangle,out int res)
{
    for (int i = 0; i < 3; i++)
    {
        for (int j = 0; j < 3; j++)
        {
            if (GetLineByIndex(i).Equals(triangle.GetLineByIndex(j)))
            {
                res = i;
                return true;
            }
        }
    }

    res = -1;
    return false;
}

由此就可以进行接下来的剖分操作了。

/// <summary>
/// 进行切耳三角剖分
/// </summary>
public List<Triangle> EarCliping()
{
    Clockwise();//进行一次顺时针排序，以保证顺序
    List<Triangle> res = new List<Triangle>();
    List<Vector2> pointsTmp = new List<Vector2>(points);
    int tmp = 10000;//避免出现错误导致死循环死机而设置的最大循环上限数
    int id = 0;
    while (pointsTmp.Count > 3 && tmp > 0)//当未剖分的顶点在三个以上时
    {
        tmp--;
        for (int i = 0; i < pointsTmp.Count; ++i)
        {
            Triangle triangle = new Triangle(pointsTmp[i - 1 < 0 ? pointsTmp.Count - 1:i-1], pointsTmp[i],pointsTmp[i + 1 >= pointsTmp.Count ? 0 : i + 1],0);//以i为中间顶点设置三角形
            
            if(triangle.GetLineByIndex(0).ClassifyPoint(triangle.center) != PointSide.LEFT_SIDE)//如果构成的三角形的中心不在线的内侧，就代表这是个凹点
                continue;
            if (!MUtil.TryGetInnerPoints(triangle,this, out List<int> inners))//如果这个三角形内没有其他点，那就是耳朵
            {
                triangle.ID = id;
                ++id;
                res.Add(triangle);//添加这个耳朵三角形
                pointsTmp.RemoveAt(i);//从原多边形中裁去
                break;
            }
        }
    }
    Triangle last = new Triangle(pointsTmp[0],pointsTmp[1],pointsTmp[2],id);//将最后三个顶点组成三角形
    res.Add(last);

    /*for (int i = 0; i < res.Count; i++)
    {
        var tri = res[i];
        for (int j = 0; j < res.Count; j++)
        {
            var triNext = res[j];
            if(tri.ID == triNext.ID)
                continue;
            if (tri.TryGetNeighbor(triNext, out int index))
            {
                tri.SetNeighbor(index,triNext.ID);
            }
            
        }
    }*/
    MUtil.FindNeiborgh(res);//将上面查找并设置邻居的代码封装到工具类中了
    return res;
}

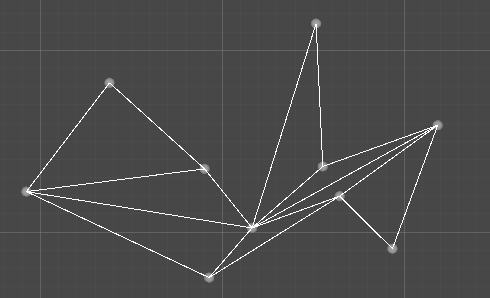
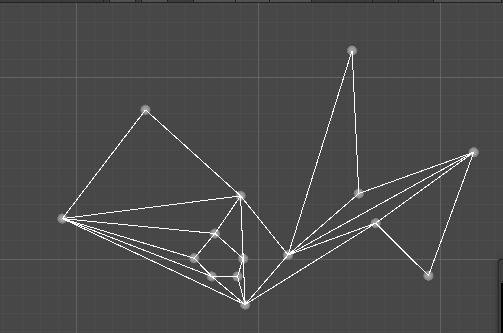
进行测试，现在已经可以获得剖分后的三角形了

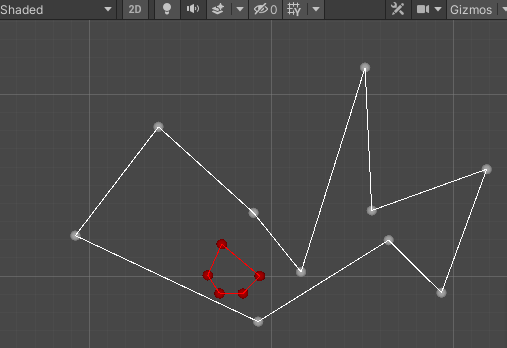
对内部有空洞的多边形进行剖分

下一步就是如果内部存在空洞的情况了，在这先只考虑简单情况，即不出现套娃型空洞。
如图所示：

那么需要做的就是先将内部空洞多边形与外部合并成简单多边形，此处则需要寻找到互相可见点。

/// <summary>
/// 寻找互相可见点
/// </summary>
public static int[] FindVisiblePoint(Polygon outer, Polygon inner)
{
    int[] ans = new int[2];//0为内部空洞的互相可见点的index，1为外部多边形的
    var xMaxPoint = inner.GetXMaxPointIndex();//遍历寻找内部多边形x值最大的点，如果x一样则找y更大的
    ans[0] = xMaxPoint;//内部多边形x值最大的点即是内部空洞的互相可见点
    outer.Clockwise();
    inner.Counterclockwise();//确认点的排布顺序（外部顺时针，内部逆时针）
    Vector2 targetPoint = inner.points[xMaxPoint] + Vector2.right * 100000;//默认当前目标点在极远处
    Vector2 crossPoint = Vector2.zero;//与线段的交点
    int targetPointIndex = 0;
    for (int i = 0; i < outer.points.Count; ++i)
    {
        Vector2 point1 = outer.points[i];
        Vector2 point2 = outer.points[i + 1 >= outer.points.Count ? 0 : i + 1];
        if (MMath.TryGetCrossWithXRay(inner.points[xMaxPoint], point1,point2, out Vector2 res))//获取向右发射的射线与目标线段的交点，如果没交点则返回false
        {
            Vector2 target = Vector2.Distance(point1, inner.points[xMaxPoint]) <= Vector2.Distance(point2, inner.points[xMaxPoint]) ? point1 : point2;
            int index = target.Equals(point1) ? i : (i + 1 >= outer.points.Count ? 0 : i + 1);
            if (Vector2.Distance(target, inner.points[xMaxPoint]) < Vector2.Distance(targetPoint, inner.points[xMaxPoint]))//如果小于之前的交点的距离
            {
                targetPoint = target;
                crossPoint = res;
                targetPointIndex = index;
            }
            
        }
    }

    if (TryGetInnerPoints(new Triangle(inner.points[xMaxPoint], crossPoint, targetPoint, 0, 0), outer, out List<int> points)
    ) //如果三角形内有其他多边形的点
    {
        int index = 0;
        Vector2 v1 = (crossPoint - inner.points[xMaxPoint]).normalized;
        float minCos = Vector2.Dot(v1, (outer.points[points[0]] - inner.points[xMaxPoint]).normalized);
        for (int j = 0; j < points.Count; ++j)//寻找与“原点”角度最小的点
        {
            Vector2 v2 = outer.points[points[j]] - inner.points[xMaxPoint];
            float cos = Vector2.Dot(v1, v2.normalized);
            if (minCos > cos)
            {
                minCos = cos;
                ans[1] = points[j];
            }
        }
        
        return ans;
    }

    ans[1] = targetPointIndex;
    return ans;
}

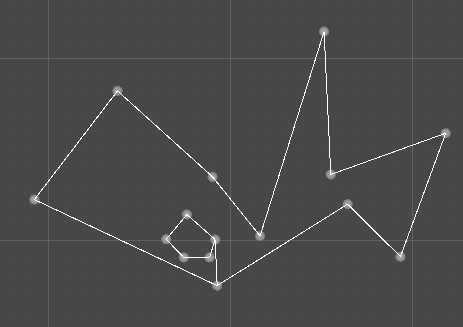
至此，就能够将内多边形与外多边形合并成简单多边形了

然后再对这个简单多边形进行剖分

就可以得到剖分后的三角形们了。

使三角形支持A*寻路

当然，目前的三角形还是不够完成寻路操作的。对于三角形的寻路一般使用的是A*算法，所以有几个关键参数需要补充到三角形上，那就是G和H，其中H这里设置为到目标的直线距离，由于此时的网格不是二维数组网格那样的规整网格，所以G的计算需要重新想方法，在这里则设置为三角形的从进入到出去所要移动的距离（进入边到离开边的中点之间的距离）。
同时，还需要保存寻路中的父节点信息，可以直接保存为父三角形的ID。
据此，创建NavTriangle继承于Triangle来实现。

public class NavTriangle : Triangle
{
    // 寻路相关参数
    public int traversalTimes;   //是否已经遍历过，可能会有多次（多个Agent）所以不设为bool
    public int parentID;    //父节点ID
    public bool isOpen;     //是否打开


    //评估相关
    public double H;   //H值
    public double G;   //G值
    public int inWallIndex; //进入边
    public int outWallIndex; //离开边

    public NavTriangle():base()
    {
        Reset();
    }

    /// <summary>
    /// 重置
    /// </summary>
    public void Reset()
    {
        this.traversalTimes = -1;
        this.parentID = -1;
        this.isOpen = false;
        this.outWallIndex = -1;
        this.H = 0;
        this.G = 0;
        this.inWallIndex = -1;
    }
}

然后在Triangle中添加public double[] neighborWallDistance;保存相邻两边的中点距离（0-1，1-2，2-0三边），在构造函数中进行计算。

到这，除了一些辅助性方法外，已经做好了A*的准备工作。

更新于：2021年3月11日

NavMesh

Navigation

自制NavMesh2D（三）

图源：https://www.pixiv.net/artworks/85447522 对三角形进行A*寻路在获得具体路径之前，需要知道走过了哪些三角形，只有知道需要经过哪些三角形才能进行接下...

自制NavMesh2D（一）

图源：https://www.pixiv.net/artworks/84705376 网格构建三角形剖分三角形剖分的方法有好几种例如Delaunay三角剖分算法 123451.除了端点，三角...