图源:https://www.pixiv.net/artworks/83559708
在有了一个简单的NavMesh后,开始回到第一步,构建多边形。
根据sprite顶点生成
由于是基于2D所制作的,所以我在这没有选择“光栅化”去获取边界,而是直接拿到sprite的顶点信息,甚至直接拿到三角形的信息,通过给其标记为寻路网格或者障碍物来控制多边形的合成(偷个懒)。
例如对于一个默认的长方形sprite其拥有顶点与三角形的信息,而这些其实可以直接利用到生成中。
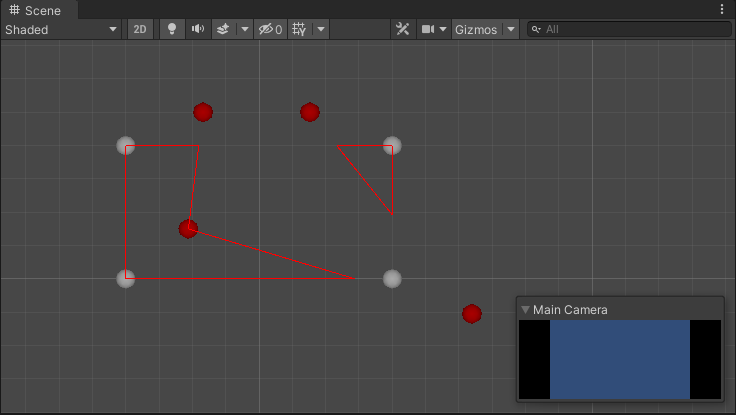
另外由于如果只是拿到顶点信息,由于其并不是按照顺时针或逆时针排序的,所以仅凭顶点是无法获取多边形数据的(对于较复杂的凹多边形而言),所以需要获得其三角形的列表,其有着顶点之间的关系信息。
其实如果只是根据这些信息生成多边形,再剖分成三角形,貌似有点多此一举(拿到三角形的信息,生成多边形,再生成三角形),所以对于不需要障碍物的NavMesh就可以直接根据这些三角形转换成需要的寻路三角形进行使用了。
当然更普遍的情况是存在障碍物甚至动态障碍物,其中动态障碍物需要能够进行局部的网格重新生成(如果重新生成整张网格其实有很大一部分没有变化,同时会造成不必要的性能开销)。同时为了尽量减少工作量(偷懒),这里我对障碍物的处理是:获取被障碍物覆盖的三角形->将这些三角形合并成多边形->进行内外多边形的合并->剖分成新的三角形列表。
那么如何获取被覆盖的三角形有哪些呢,由于我没在网上搜到类似资料,所以采用的是最粗暴的遍历法——多变形的每条边与没有检测到的三角形的边检测是否相交,如果相交则将该边对应的两个三角形加入合并列表。
然后以合并列表中的三角形的一条无邻居的边(以保证该边不是多边形内部边)的起点为起点,绕边缘描绘出多边形。
例如在下面这个合并三角形列表中,以b边的起点B作为遍历起点,然后找到其终点C,再以C为起点找到D······,就能够描绘出这些三角形构成的多变形了。(此处都已规定除障碍物/内部多边形外都是顺时针排布)
对于这个构造出来的多边形,再使用内外多边形合并的操作,然后进行剖分,就能够得到新的三角形列表了,最后再将这些三角形添加回原三角形列表,更新三角形的相邻关系与ID即可。
对于越界的障碍物
障碍物可不会老老实实待在多边形内部,更常见的情况是障碍物会与多边形边界相交。
如下面绿色的障碍物有一部分再白色地面的外部。

那么此时要做的就是将这块覆盖的区域“剔除”。
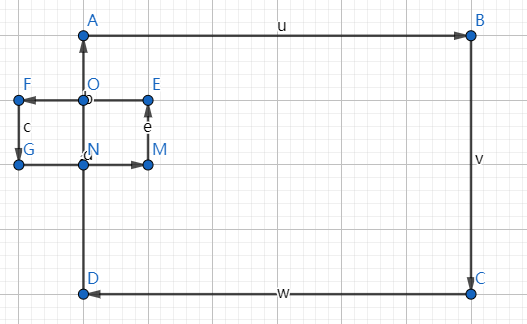
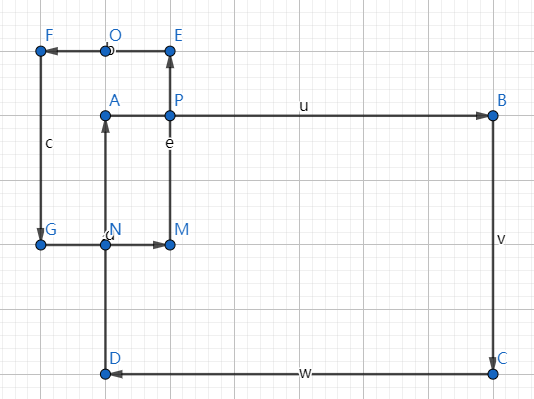
先从这种最简单的情况考虑,可以看出边界与障碍物的边交于两点,那么剔除后的多边形应为A->B->C->D->N->M->E->O->A。
此时规定障碍物与多边形的方向相反的好处再次体现出来了,能够根据交点很方便得获得增添的新顶点。
添加顺序为离边界起点(这里是D)近的边(这里是GM)的起点、交点(这里是N)、终点(M)、内部顶点、较远的边(EF)重复GM的顺序。
如果多边形的顶点在障碍物的内部的话,则需将该顶点删去。
简单的写个脚本来测试
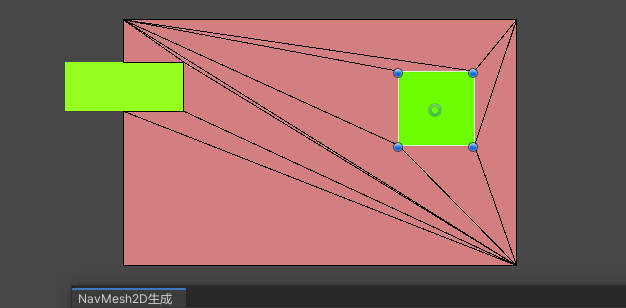
可以看到已经能够正确剔除了。
换个情况
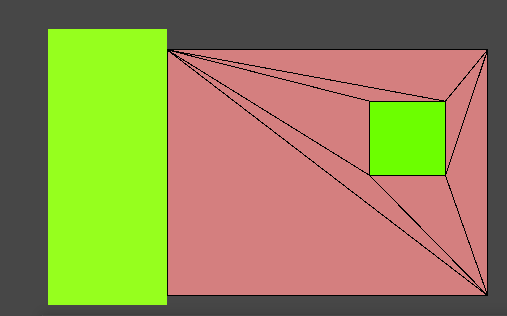
对于分割了多边形的障碍物
还有种情况,那就是一个障碍物分割开了多边形,那么上面这种方法就不行了。
在搜索了资料后,最相似的情况便是图形学中的三角形裁剪,可是情况不一样的是一个是求两多边形的交集,一个是求补集,但其思路是差不多的,问题就在于如何找到点之间的关系。
这里参考了任意多边形切割/裁剪使用链表进行分割的思路。
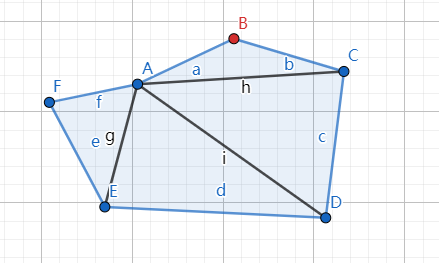
如该图所示的障碍物(EFGH)将多边形(ABCD)分割成了两块,分别是A->e1->e2->D 和 B->C->e3->e4。
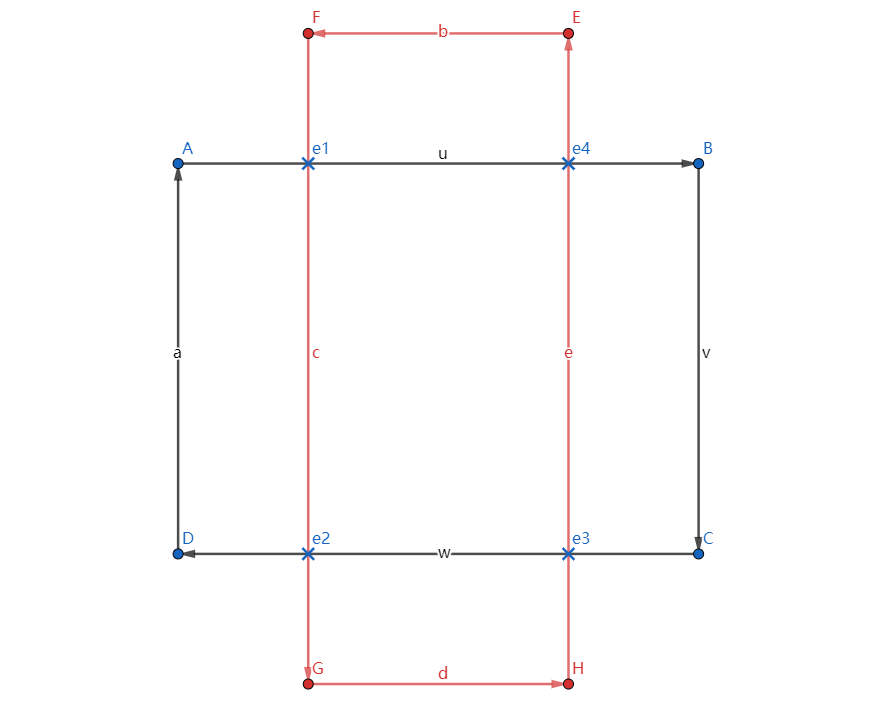
用链表图表示其中一部分变化就是由

变成了
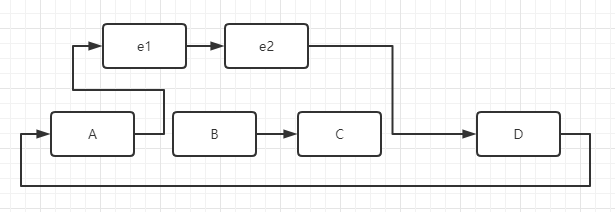
看得出插入位置在交点所在线的端点中间,且端点为起点还是终点与插入的方向是有关的。如果端点是起点,那么是端点连接交点,如果是终点,则是交点连接端点。
如果相邻交点的连线在多边形内,则连接上,而由于多边形规定为顺时针,障碍物为逆时针,所以可以根据相交边的方向来判断。
综上两点,举例:
1、F->G与A->B交于e1:
如果从障碍物的边的终点看向起点,相交边的起点在左侧,将交点e1插入F->G间,可以得知左侧端点为起点,那么将A连接上e1,同时根据相交线段的方向知道是进入多边形,所以将交点放入栈暂存。
2、F->G与C->D交于e2:
如果从障碍物的边的终点看向起点,相交边的终点在左侧,将交点e2插入e1->G间,可以得知左侧端点为终点,那么将e2连接上D,同时根据相交线段的方向知道是离开多边形,如果此时栈内有交点,取出并将该交点(e1)连接上e2。
由此就构建出了一个由循环链表构成的多边形A->e1->e2->D了,B->C->e3->e4同理。
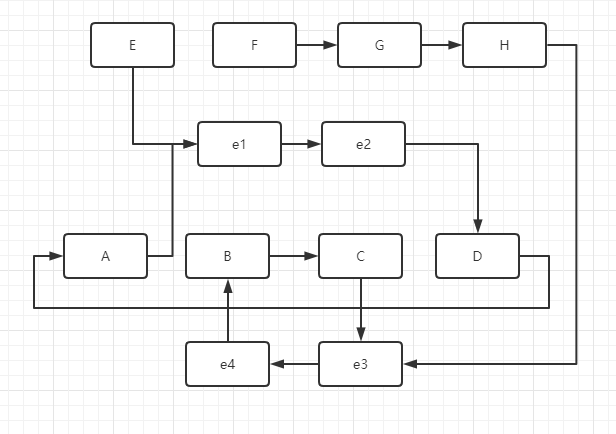
通过遍历多边形的顶点,解构出两个循环链表便是所需的多边形了。
可以看到上图将障碍物的顶点链表也包含进来了,原因是有种情况即障碍物的顶点在多边形内部时,需要将该顶点包含进来,而使用链表即可很好解决这些包含进来的顶点之间的关系。
这块代码写得有点乱完整版就暂时不贴了(
核心代码
1 | public List<Polygon> Clips(Polygon ob) |
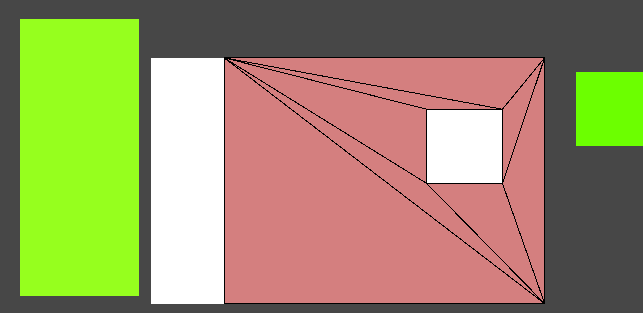
再简单的写个测试脚本验证下:
白色矩形为多边形,红色为障碍物。
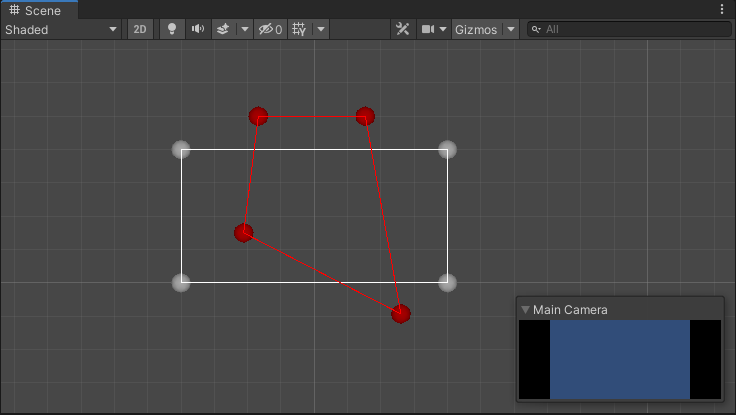
进行切割后
如果障碍物遮住了多边形顶点的情况: